Motivation

A significant number of proteins have been found experimentally to fold via a two-state process in which only the fully unfolded and native states are ever populated. Our approach assumes two states in the protein folding process: early-stage and late-stage folding. The two-states are closely related with the idea of the reduced conformational space for early-stage protein folding. The complete conformational space is available after reaching the proper conformation determined in a first step of folding. The existence of the first step determines to some extent the search for the final native conformation.

Defining conformational subspace

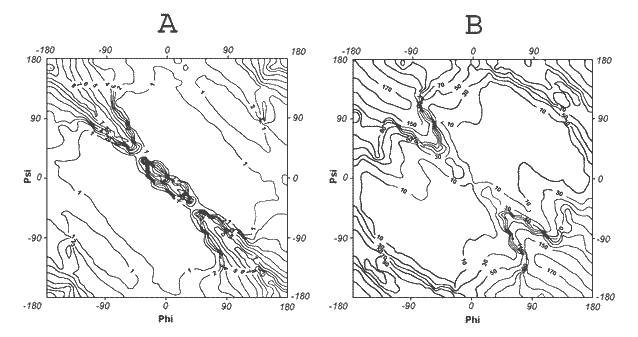
The early-stage folding was built on the characteristics of the polypeptide chain treated as a chain of rigid peptide planes, which can create shapes with different radii of curvature depending on the dihedral angles between two sequential peptide bond planes (V-angles) polypeptide conformations can be treated as helicoidal. β-Structure represents the helical structure characterised by an infinitely large radius of curvature. It turned out that the V-angle can change form 0° (parallel mutual orientation) to 180° (anti-parallel orientation) allowing creation of a very squeezed helix (V-angle close to zero); then an increase of the V-angle causes an increase of the R-radius of curvature, reaching R infinitely large for the β-structure and extended. Instead of the φ,ψ conformational space, the V-R conformational space can be used for polypeptide structure representation. Using the above defined geometric parameters, the Ramachandran map can be interpreted as shown in Fig.1. Fig.1A shows the distribution of the R,-radius of curvature (on log scale) for polypeptide fragments (pentapeptides) all over the conformational space. The distribution of V-angles is shown in Fig.1B.

Fig. 1.	Distribution of geometrical parameters all over the Ramachandran map.
	A   dihedral angle, V, between two sequential peptide bond planes,
	B   radius of curvature, R, on natural logarithmic scale.

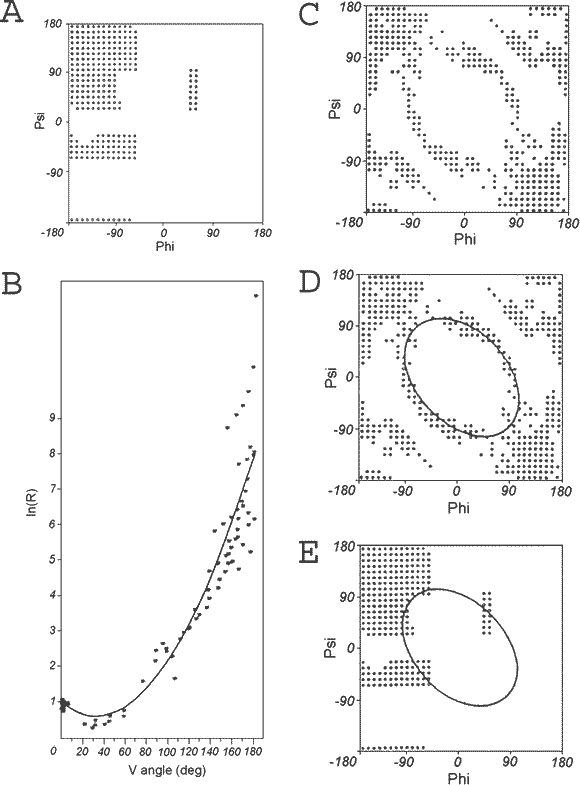
When only low-energy conformations (Fig.2A) are taken into account, the dependency of R (log scale) on the V-angle can be approximated to a second-degree polynomial function (Fig.2B and Eq.1).

Eq.1:

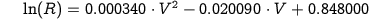
On the other hand, the distribution of points that satisfy the presented dependency (Fig.2A) is represented as shown in Fig.2C. A convenient way to search for low-energy conformations seems to be the ellipse-shaped curve shown in Fig.2D and Eq.2, which links all low-energy conformations very nicely (Fig.2E).

Eq.2:

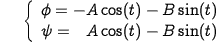
Fig. 2.	Ellipse path determination.
	A   φ,ψ map with low-energy area distinguished,
	B   ln(R) as a function of V angle for grid points shown in A,
	C   Ramachandran map with grid points, where the structure satisfies Eq.1,
	D   low-energy areas linked by ellipse.

In consequence, a geometric analysis of the polypeptide chain limited to simple R(V) representations prompts the limited conformational sub-space, which can be treated as the early-stage folding (in silico) conformational sub-space. This accords with the generally accepted assumption that the backbone conformation is responsible for the early-stage folding step.

Independent support for the model from elements of information theory

It turned out, that limited conformational sub-space balances the amounts of information stored in the amino acid sequence and needed for structure prediction .The balance between the amount of information stored in the nucleotide (tri-nucleotide) appeared to be comparable with the amount of information necessary to determine the amino acid from among twenty of them. The same idea was applied for the relation between the amount of information carried by an amino acid and the amount of information necessary to predict a particular conformation determined by φ,ψ angles (a point on the Ramachandran map).

The amount of information [bit] carried by a particular amino acid can be calculated using Shannon's equation:

Eq.3:

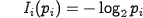
where p_i expresses the probability of the i-th amino acid's presence in a sequence (approx. p = 1/20).

The amount of information necessary to predict a particular φ,ψ angle can be calculated according to the same equation with p equal to the probability of the occurrence of these angles (which is much lower than 1/20). The entropy of information measuring the averaged amount of information necessary to predict structure with 1x1° precision can be calculated for each amino acid as follows:

Eq.4:

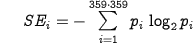
where p_i represents the probability of occurrence of particular φ,ψ angles (which can be calculated for PDB).

These quantities were calculated (taking into account the different frequencies of particular amino acids and the probability distribution all over the Ramachandran map). Eq.4 applied to the ellipse-limited conformational sub-space leads to equilibration between these two quantities (Tab.1).

It can be proved that the large disproportion between these two events for the whole Ramachandran map makes the problem unsolved. Limitation of the conformational space (Ramachandran map) to the sub-space (for example the ellipse path) balances these two quantities. The amount of information carried by an amino acid (calculated according to its frequency) and the amount of information (entropy of information) necessary to predict the fragment of the ellipse (10°) becomes comparable (Tab.1).

Amino- acid	Amount of information [bit]
	carried by an aminoacid	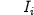necessary to predict the ellipse-belonging structure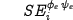
GLY	3.805	5.740
ASP	4.117	5.016
LEU	3.492	4.437
LYS	3.908	4.764
ALA	3.662	4.462
SER	4.095	4.857
ASN	4.545	5.186
GLU	3.833	4.550
THR	4.196	4.579
ARG	4.249	4.650
VAL	3.886	4.108
GLN	4.663	4.667
ILE	4.151	4.115
PHE	4.713	4.528
TYR	4.941	4.574
PRO	4.442	4.062
HIS	5.477	4.868
CYS	5.544	4.792
MET	5.614	4.484
TRP	6.236	4.512

Tab.1. The amount of information carried by an individual amino acid in relation to
the amount of information necessary to predict the fragment of the ellipse (10°).